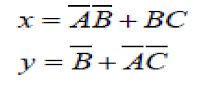استخدام الجبر البولياني في تصميم الدارات المنطقية

استخدام الجبر البولياني في تصميم الدارات المنطقية 

في عصر الأنظمة الرقمية والذي يتركز على اجتياح الدارات المنطقية على اغلب النشاطات التي تمثلها الأنظمة الرقمية، فكافة هذه الأنظمة تحتوي على عدة دوائر منطقية التي تنفذ بعض العمليات الأساسية  التي تكرر تنفيذها وبسرعة كبيرة التي تسمى أيضا بالبوابات المنطقية،هذه البوابات تمُثل الأساس لعمل أي دائرة منطقية فهي بوابة تعطي خرج البيانات عندما تحقق شروط معينة على هذه المدخلات.وسوف نبين في هذا البحث المبسط استخدامات الجبر البوليني في تصميم البوابات المنطقية. 

الجبر البولياني 

 طريقة رياضية تستعمل لحل مسائل المنطق والاحتمالات الهندسية , سميت هذه الطريقة باسم جورج بول وهو عالم منطق ورياضيات  إنجليزي , وقد طور بول طريقة لتكوين العبارات المنطقية بالرموز , يختلف جبر بول عن الجبر العادي في أن متحولات وثوابت جبر بول تأخذ قيمتين فقط وهما  ("1" , "0") وإن هذه القيم التي يأخذها المتحول  المنطقي لا تعبر في الحقيقة عن قيم واقعية وإنما عن حالة يمثلها المتحول ويمكن أن تسمى مثلاً صح أو خطأ ، عالي أو منخفض ..... الخ .

وبما أن جبر بول يتعامل مع قيمتين فقط فلا يوجد في جبر بول طرح أو قسمة أو جذر تربيعي أو فواصل أو أرقام سالبة أو تربيع أو تكعيب أو لوغاريتمات .

توجد فقط  ثلاث عمليات أساسية :

• الجمع المنطقي Logical addition ويرمز لها بنفس إشارة الجمع العادي (+) و تسمى أيضاً عملية OR
• الضرب المنطقي Logical multiplication ويرمز لها بنفس إشارة الضرب العادي ( . ) و تسمى أيضاً عملية AND 
• المتمم المنطقي Logical complementation  ويرمز لها بإشارة المتمم ( ¯¯¯ )  و تسمى أيضاً عملية NOT 

الدارات المنطقية

 و تسمى أيضاً  ( الشبكات المنطقية ) وهي هياكل تبنى من بعض الدوائر البدائية التي تسمى بوابات منطقية , كل دائرة منطقية تحتوي على  واحد أو أكثر من أجهزة الإدخال و واحد فقط من أجهزة الإخراج , حيث تقوم بعملية منطقية على المدخل وتنتج المخرج المطلوب تستخدم هذه البوابات في بناء معالجات الأجهزة الالكترونية والحواسيب لأن مخرج البوابة الرقمية هو أيضاً  قيمة منطقية , فإنه يمكن استخدام مخرج أحد البوابات المنطقية كمدخل لبوابة أخرى  يتم صناعة هذه الدائرة الالكترونية للبوابة الرقمية باستخدام ديودات وترانزستورات و يمكن أيضاً بناؤها باستخدام المبدلات الالكترونية , سوائل منطقية  , إشارات ضوئية , وحتى من أجزاء ميكانيكية  . 

  بناء الدوائر المنطقية : 

بعد تبسيط التعبيرات المنطقية تأتي الخطوة الأخيرة في عملية تصميم الدوائر المنطقية ألا و هي بناء الدائرة المنطقية. والبناء هنا إما أن يتم باستخدام البوابات الأساسية الثلاث (AND , OR , NOT)  و إما أن يتم باستخدام نوع واحد  فقط من البوابات ( إما NAND أو NOR )

 أولا : 

 البناء باستخدام البوابات الأساسية الثلاث :

إن شكل الدائرة المنطقية يعتمد على الصورة التي كتبت بها التعبيرات المنطقية . فالتعبيرات المكتوبة في صورة مجموع الحدود الصغرى ينتج عنها دائرة في شكل AND-OR Structure , أما التعبيرات المكتوبة في صورة مضروب الحدود الكبرى فينتج عنها دائرة في شكل OR-AND Structure  

 مثال :

 استخدم البوابات الأساسية الثلاث (AND , OR , NOT) في بناء الدائرة المنطقية الممثلة بالتعبيرين المختصرين التاليين المكتوبين في صورة مجموع الحدود الصغرى

الحل :

ثانياً :

 البناء باستخدام نوع واحد فقط من البوابات : 

عندما يتم تصنيع الدائرة المنطقية في شكل دائرة متكاملة ( Integrated Circuit ) أو IC  فإنه عادة ما يتم بناء الدائرة المنطقية بالكامل باستخدام نوع واحد فقط من البوابات. و البوابات المستخدمة هنا إما أن تكون بوابات Nand أو بوابات Nor 

البناء باستخدام بوابات Nand : 

يجب أن تكون التعبيرات المنطقية مكتوبة في صورة مجموع الحدود الصغرى للحصول على AND-OR Structure , ثم يتم بعد ذلك تحويل AND-OR  Structure إلى دائرة مبنية بالكامل من بوابات NAND كالتالي : 

حيث نقوم بإجراء عملية عكس منطقي مرتين متتاليتين ،  مرة في خرج بوابة AND  و مرة في خرج بوابة OR , والعكس المنطقي مرتين متتاليتين ، كما نعلم , لا يغير من قيمة المتغير لأن 

 ثم نستبدل بوابة OR  التي تم OR عكس جميع أطراف الدخل لها ببوابة NAND , لأن عملية OR مسبوقة بعكس الدخل تكافىْ عملية NAND ، أي أن :

عبارة عن تحويل ال AND-OR Structure إلى دائرة مبنية بالكامل من بوابات NAND فإننا نقوم باستبدال جميع العواكس المنطقية ببوابات NAND , و استبدال جميع بوابات AND ببوابات NAND , و استبدال جميع بوابات OR  ببوابات NAND , أي نقوم ببساطة باستبدال أي بوابة بال AND-OR Structure ببوابة NAND  لها نفس عدد أطراف الدخل .

و هناك مشكلة صغيرة قد تواجهنا عند تحويل ال AND-OR Structure الى دائرة مبنية بالكامل من بوابات NAND , و تتضح هذه المشكلة في الدارة التالية : 

نلاحظ هنا أن المتغير C  يدخل مباشرة إلى بوابة OR  دون أن يكون خارجاً من بوابة AND  و لتحويل الدائرة الى دائرة مبنية بالكامل من بوابات NAND  نحتاج لإجراء عملية عكس منطقي في كل طرف من أطراف الدخل لبوابة OR حتى نقوم بتحويلها الى بوابة NAND  و نقوم بإلغاء تأثير هذا العكس المنطقي بإجراء عكس منطقي آخر في خرج بوابة AND  لإجراء عملية عكس منطقي في خرجها لمعادلة العكس المنطقي الذي تم في دخل بوابة OR 

يتم حل هذه المشكلة كالتالي : 

قمنا هنا بإضافة بوابة  NAND  ذات طرف دخل واحد لتقوم بإجراء عملية عكس منطقي تعادل عملية العكس المنطقي التي تمت في دخل بوابة OR  و يمكن الاستغناء عن بوابة  NAND  ذات طرف الدخل الواحد هذه إذا توفر معكوس المتغير الذي يدخل مباشرة إلى بوابة OR , حيث نقوم بإدخال هذا  المعكوس مباشرة إلى بوابة NAND  . 

مثال : 

قم ببناء الدائرة المنطقية الممثلة بالتعبيرين المنطقيين المختصرين التاليين باستخدام بوابات NAND فقط 

الحل : 

ثم نقوم باستبدال جميع البوابات بالدائرة ببواباتNAND بنفس عدد أطراف  الدخل , مع مراعاة عكس المتغير الذي يدخل مباشرة إلى بوابة OR 

البناء باستخدام بوابات NOR : 

يجب أن تكون التعبيرات المنطقية مكتوبة في صورة مضروب الحدود الكبرى للحصول على OR-AND Structure ثم يتم بعد ذلك تحويل ال OR-AND Structure الى دائرة مبنية بالكامل من بوابات NOR كالتالي : 

• يتم استبدال كل عاكس منطقي ببوابة  NOR  ذات طرف دخل واحد

• يتم تحويل بوابات OR  مع بوابات AND  الى بوابات NOR كالتالي : 

حيث نقوم بإجراء عملية عكس منطقي مرتين متتاليتين ،  مرة في خرج بوابة OR و مرة أخرى في دخل بوابة AND ، ثم نستبدل بوابة AND التي تم عكس جميع أطراف الدخل لها ببوابة NOR ، لأن عملية AND مسبوقة بعكس الدخل تكافىْ عملية NOR 

أي أن :

أي أنه لتحويل ال OR-AND Structure الى دائرة مبينة بالكامل من بوابات NOR  فإننا نقوم ببساطة باستبدال أي بوابة ببوابة NOR لها نفس عدد أطراف الدخل .

و في حالة دخول متغير مباشرة الى بوابة AND نقوم بإدخال معكوس ذلك المتغيرالى بوابة NOR التي حلت محل بوابة AND .

مثال :

قم ببناء الدائرة المنطقية الممثلة بالتعبيرين المنطقيين المختصرين التاليين باستخدام بوابات NOR فقط  

ثم نقوم باستبدال جميع البوابات بالدائرة ببوابات NOR